Indici de refractie. Definitii. Proprietati.
1. Definirea indicilor de refractie relativi si absoluti in optica geometrica
Refractia simpla este fenomenul de modificare a directiei de proare a luminii la traversarea suprafetei de separare a doua medii transparente omogene si izotrope, distincte. Intr-un mediu se proa raza incidenta iar in celalalt mediu raza emergenta refractata.
In acord cu principiul reversibilitatii razelor de lumina, geometria razei nu se schimba la proarea luminii in sens invers. Raza incidenta se proa acum in al doilea mediu iar raza emergenta , in primul pe acelasi drum. In optica geometrica, intersectia razei incidente considerate cu suprafata de separare a celor doua medii defineste punctul de incidenta. Perpendiculara in acest punct pe ul tangent la suprafata de separare in acelasi punct, reprezinta asa zisa normala la suprafata de separare in punctul de incidenta. Pentru o incidenta care nu este normala (adica pe directia normalei), raza incidenta (sau refractata) si normala in punctul de incidenta determina asa zisul de incidenta (sau de refractie). Unghiul dintre raza incidenta (respectiv refractata) si normala se numeste unghi de incidenta (respectiv refractie), si se noteaza cu i (respectiv r); daca mediul de incidenta (respectiv refractie) se numeroteaza cu 1 (respectiv 2), unghiul de incidenta (respectiv refractie) se poate nota cu i1 (respectiv i2) (. 1)
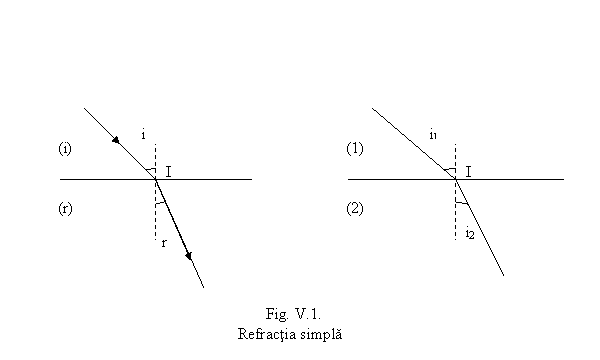
In optica geometrica, fenomenul de refractie este guvernat de urmatoarele doua legi empirice:
I. Raza refractata se afla in acelasi cu raza incidenta si normala, de partea opusa razei incidente fata de normala
II. Raportul dintre sinusul unghiului de incidenta si sinusul unghiului de refractie este o marime constanta pentru o pereche specificata de medii transparente, omogene si izotrope care se numeste indice de refractie relativ al mediului de refractie fata de cel de incidenta,
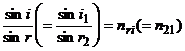 (1.)
(1.)
Din definitie rezulta ca indicele de refractie este o marime adimensionala. Din definitia indicelui de refractie relativ in optica geometrica rezulta ca:
![]() (2.)
(2.)
Observatie:
Daca se ia in consideratie natura ondulatorie electromagnetica a
luminii si razele opticii geometrice se considera monocromatice,
atunci, asa cum se constata experimental, indicele de refractie
poate depinde de frecventa (sau pulsatia ![]() ) razei. Aceasta dependenta este
caracteristica fenomenului de dispersie a luminii. In acord cu datele
experimentale, de regula se considera ca la trecerea razei
dintr-un mediu optic in altul, frecventa razei nu se modifica.
Indicele de refractie al unu mediu fata de vid se numeste
indice de refractie absolut al acelui mediu (si pentru mediile
1((i))) respectiv 2((r)) indicii de refractie absoluti se
noteaza cu n1 (ni) respectiv n2 (nr).
In consecinta indicele de refractie absolut al vidului este egal
cu unitatea (deoarece la trecerea din vid in vid nu se produce refractie,
i2 = i1). Este simplu de vazut ca indicele
relativ al mediului (2) fata de mediul (1) este egal cu raportul
indicilor absoluti ai celor doua medii:
) razei. Aceasta dependenta este
caracteristica fenomenului de dispersie a luminii. In acord cu datele
experimentale, de regula se considera ca la trecerea razei
dintr-un mediu optic in altul, frecventa razei nu se modifica.
Indicele de refractie al unu mediu fata de vid se numeste
indice de refractie absolut al acelui mediu (si pentru mediile
1((i))) respectiv 2((r)) indicii de refractie absoluti se
noteaza cu n1 (ni) respectiv n2 (nr).
In consecinta indicele de refractie absolut al vidului este egal
cu unitatea (deoarece la trecerea din vid in vid nu se produce refractie,
i2 = i1). Este simplu de vazut ca indicele
relativ al mediului (2) fata de mediul (1) este egal cu raportul
indicilor absoluti ai celor doua medii:
![]() (3.)
(3.)
Intr-adevar,
daca cele doua medii (1) si (2) se separa printr-un strat
-paralel vid ((0)) geometria razelor incidenta in mediul (1) si
refractata in mediul (2) nu se modifica deoarece unghiul de
refractie pentru perechea ((1),(0)) este egal cu unghiul de
incidenta pentru perechea ((0),(2)). (. 2)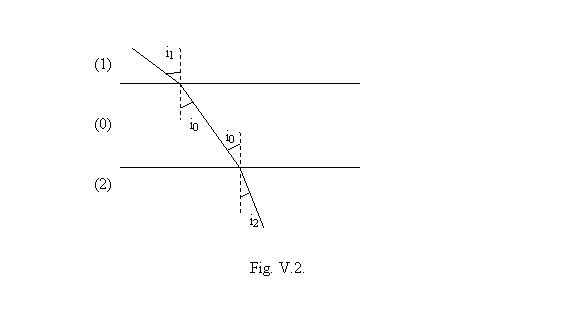
Folosind principiul reversibilitatii razelor de lumina se obtine succesiv:
![]() ,
, ![]() ,
, ![]()
2 Forma Snell Dessectiunes a legii a II- a a refractiei
Substituind relatia (3) in relatia (1) se obtine succesiv
![]()
![]() (4.)
(4.)
Ultima relatie (4.) poate fi generalizata simplu in cazul unui sistem de mai multe straturi -paralele adiacente succesiv de medii transparente cu indicii de refractie absoluti n1, n2, n3 (. 3.). Aceasta generalizare poarta numele autorilor (numindu-se legea Snell Dessectiunes a refractiei) si are exprimarea
![]() (5)
(5)
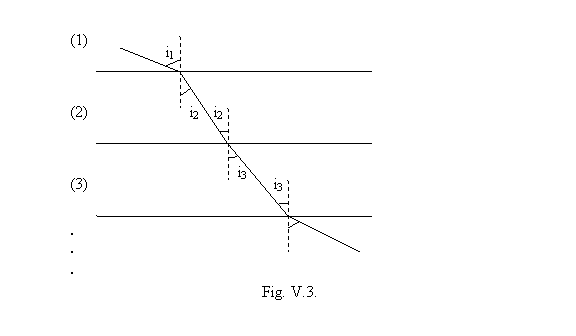
Relatia (5) se obtine simplu folosind relatiile de tip (4) pentru perechile de medii ((1),(2)), ((2),(3)) s.a.m.d. si constatand ca fiecare pereche de relatii succesive contine un termen comun:
![]() ,
, ![]()
Rezulta astfel egalitatile (5).
Legea Snell Dessectiunes a avut un rol important in identificarea drumului optic ca invariant integral al opticii geometrice, descoperirea principiului egalitatii drumurilor optice (Malus - Dupin) conform caruia, indiferent de mediile optice si de suprafetele de discontinuitate strabatute, drumurile optice dintre doua suprafete de unda oarecare sunt egale pentru toate razele de lumina si formularea principiului lui Fermat care arata ca traiectoria reala a razei de lumina reprezinta o solutie extremala sau stationara pentru drumul optic.
Aceste legi au permis o abordare generalizata, unitara a opticii geometrice, extrem de eficienta in descrierea si proiectare sistemelor optice cu componente simple omogene si izotrope precum si a sistemelor optice cu componente neomogene si neizotrope.
In final
mentionam ca daca ![]() , atunci
caracterizam al doilea mediu optic ca fiind mai refringent decat primul
(sau echivalent, primul mediu apare ca mai putin refringent decat al
doilea). Relatia premisa
, atunci
caracterizam al doilea mediu optic ca fiind mai refringent decat primul
(sau echivalent, primul mediu apare ca mai putin refringent decat al
doilea). Relatia premisa ![]() si legea Snell
Dessectiunes
si legea Snell
Dessectiunes ![]() implica
implica ![]() ; deoarece
; deoarece ![]() este o functie
strict crescatoare pentru
este o functie
strict crescatoare pentru ![]() , deducem de aici inegalitatea
, deducem de aici inegalitatea ![]() . Astfel la trecerea
dintr-un mediu in altul mai refringent, raza refractata se apropie de
normala. Analog rezulta ca la trecerea dintr-un mediu in altul
mai putin refringent raza refractata se indeparteaza de
normala.
. Astfel la trecerea
dintr-un mediu in altul mai refringent, raza refractata se apropie de
normala. Analog rezulta ca la trecerea dintr-un mediu in altul
mai putin refringent raza refractata se indeparteaza de
normala.
In
ultimul caz este deci posibil ca ![]() pentru
pentru ![]() ; pentru incidente
; pentru incidente ![]() se produce fenomenul de
reflexie totala, nu de refractie; raza incidenta nu mai
traverseaza suprafata de separare ci se reflecta.
Determinam l definit ca
incidenta pentru care unghiul de refractie este egal cu
se produce fenomenul de
reflexie totala, nu de refractie; raza incidenta nu mai
traverseaza suprafata de separare ci se reflecta.
Determinam l definit ca
incidenta pentru care unghiul de refractie este egal cu ![]() , adoptand conventia ca mediul de incidenta
mai refringent sa fie notat cu indicele 2. (. 4.)
, adoptand conventia ca mediul de incidenta
mai refringent sa fie notat cu indicele 2. (. 4.)
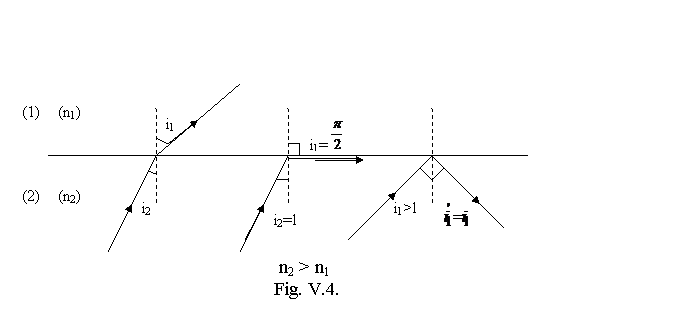
Din
conditia ![]() si legea Snell
Dessectiunes
si legea Snell
Dessectiunes ![]() deducem:
deducem:
![]() ,
, ![]() ,
, ![]() (6.)
(6.)
3 Semnificatia indicilor de refractie in optica ondulatorie
Legea Snell Dessectiunes, care este o lege empirica in optica geometrica, poate fi construita deductiv in abordarile ondulatorii ale opticii geometrice conditionate de aplicarea principiului Huygens, precum si in abordarile de electrodinamica bazate pe proprietatile undelor electromagnetice.
Considerand
primele abordari, amintim ca, in acord cu principiul lui Huygens,
proarea luminii intr-un mediu se face ca si cum toate punctele mediului
atinse de frontul de unda la un moment dat, t, devin surse de unde secundare, astfel ca la momentul
ulterior ![]() , frontul de unda coincide cu suprafata
infasuratoare a undelor secundare proate inainte (adica
pe directii inclinate numai sub unghiuri ascutite fata de
normalele locale la frontul de unda), nu si inapoi. (Ultima precizare
evidentiaza ca principiul Huygens este un postulat specific
opticii). In mediile omogene si izotrope undele secundare sunt sferice
si fronturile de unda sunt infasuratoare succesive ale
undelor secundare succesive care se proa omogen si izotrop, astfel
ca frontul de unda isi pastreaza forma generica
initiala. In acest context sa consideram refractia
unei unde e (cu frontul de unda ) la traversarea unei
suprafete e care separa doua medii optice omogene si
izotrope. Notam vitezele de faza ale undelor e in mediile (1)
si (2) cu v1, respectiv v2 (presupunand pentru
precizarea problemei ca
, frontul de unda coincide cu suprafata
infasuratoare a undelor secundare proate inainte (adica
pe directii inclinate numai sub unghiuri ascutite fata de
normalele locale la frontul de unda), nu si inapoi. (Ultima precizare
evidentiaza ca principiul Huygens este un postulat specific
opticii). In mediile omogene si izotrope undele secundare sunt sferice
si fronturile de unda sunt infasuratoare succesive ale
undelor secundare succesive care se proa omogen si izotrop, astfel
ca frontul de unda isi pastreaza forma generica
initiala. In acest context sa consideram refractia
unei unde e (cu frontul de unda ) la traversarea unei
suprafete e care separa doua medii optice omogene si
izotrope. Notam vitezele de faza ale undelor e in mediile (1)
si (2) cu v1, respectiv v2 (presupunand pentru
precizarea problemei ca
v1>
v2). Conform . 5 portiunea ![]() a frontului incident
se proa, pe baza mecanismului Huygens, cu viteza v1 pe directia normala pe
frontul de unda .
a frontului incident
se proa, pe baza mecanismului Huygens, cu viteza v1 pe directia normala pe
frontul de unda .
Pe
masura ce punctele frontului ating suprafata de separare a celor
doua medii, pe aceasta se activeaza surse secundare de unde sferice
de la care lumina se proa in mediul al doilea.
Infasuratoare momentana a suprafetelor de unda
pentru acestea determina frontul de unda momentan in al doilea mediu
care are tot caracter , dar directia de proare a noului front de
unda difera de cea din primul mediu deoarece viteza de proare
este alta, v2. Am presupus v2
< v1, deci in timpul ![]() in care lumina
se proa de la
in care lumina
se proa de la ![]() la
la ![]() in primul mediu, va strabate o distanta
in primul mediu, va strabate o distanta ![]() in mediul al doilea.
Frontul
in mediul al doilea.
Frontul ![]() este perpendicular pe directia de proare si
deci, se proa pe noua directie
este perpendicular pe directia de proare si
deci, se proa pe noua directie ![]() .
.
Frontul de
unda care la momentul t era in
pozitia ![]() in primul mediu,
capata la momentul
in primul mediu,
capata la momentul ![]() pozitia
pozitia ![]() in mediul al doilea.
in mediul al doilea.
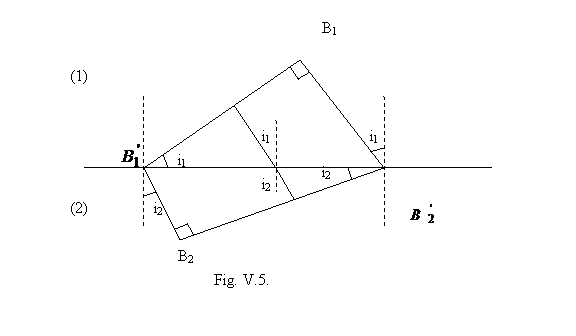
Folosind relatiile
![]() v1Δt,
v1Δt, ![]()
si
geometria evidenta triunghiurilor dreptunghice ![]() ,
, ![]() cu ipotenuza
cu ipotenuza ![]() comuna se
obtine succesiv:
comuna se
obtine succesiv:
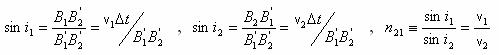
Indicele de refractie relativ al mediului (2) fata de mediul (1) este egal cu raportul dintre viteza de proare a luminii in mediul (1) si viteza de proare a luminii in mediul (2).
La trecerea in mediul (2), razele se apropie de normala deoarece viteza luminii in noul mediu este mai mica decat viteza luminii in primul mediu.
In particular, notand cu c viteza luminii in vid, obtinem exprimarea similara a indicilor de refractie absoluta (adica ai celor doua medii fata de vid),
![]()
cu satisfacerea relatiei
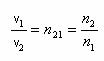
Deoarece pentru orice mediu material e
satisfacuta relatia v![]() , se obtin relatiile
, se obtin relatiile ![]() ,
, ![]()
![]() . De regula, mediile (solutiile) mai dense sunt mai
refringente, viteza luminii in acestea fiind mai mica decat viteza acesteia in
medii mai putin dense.
. De regula, mediile (solutiile) mai dense sunt mai
refringente, viteza luminii in acestea fiind mai mica decat viteza acesteia in
medii mai putin dense.
4 Exprimarea vitezei luminii si a indicilor de refractie in optica electromagnetica
Ecuatiile lui Maxwell, care sunt ecuatiile de baza ale electrodinamicii, admit si in vid, in absenta substantei, a surselor, solutii netriviale de tip unda. Din ecuatia undelor electromagnetice construita in acest context prin identificarea patratului vitezei luminii in vid din ecuatia undelor cu constanta care se structureaza in ecuatia similara pe baza ecuatiilor Maxwell, rezulta urmatoarele exprimari ale vitezelor undelor electromagnetice si implicit optice:
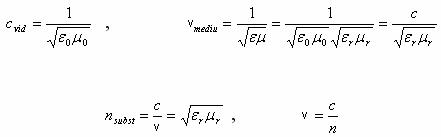
unde ![]() si
si ![]() sunt
permitivitatile electrice absolute pentru vid respectiv pentru mediul
de substanta considerat,
sunt
permitivitatile electrice absolute pentru vid respectiv pentru mediul
de substanta considerat, ![]() fiind permitivitarea
relativa a mediului, iar
fiind permitivitarea
relativa a mediului, iar ![]() si
si ![]() sunt
permeabilitatile magnetice pentru vid, respectiv pentru mediu,
sunt
permeabilitatile magnetice pentru vid, respectiv pentru mediu, ![]() fiind permeabilitatea
magnetica relativa a mediului.
fiind permeabilitatea
magnetica relativa a mediului.
Constantele ![]() si
si ![]() si implicit
viteza undelor electromagnetice in vid, c, nu depind de frecventa
acestora. In schimb permitivitatile electrice
si implicit
viteza undelor electromagnetice in vid, c, nu depind de frecventa
acestora. In schimb permitivitatile electrice ![]() si permeabilitatile magnetice
si permeabilitatile magnetice ![]() absolute si
implicit cele relative pot depinde sensibil de frecventa undelor
electromagnetice astfel ca viteza undelor in mediul material vmediu
absolute si
implicit cele relative pot depinde sensibil de frecventa undelor
electromagnetice astfel ca viteza undelor in mediul material vmediu![]() si implicit
lungimea de unda
si implicit
lungimea de unda![]() si
indicele de refractie n pot
depinde de frecventa. Aceasta dependenta
defineste fenomenul de dispersie.
Mediile materiale pentru care aceasta dependenta nu poate fi
neglijata in intervalul optic de frecvente se numesc medii dispersive.
si
indicele de refractie n pot
depinde de frecventa. Aceasta dependenta
defineste fenomenul de dispersie.
Mediile materiale pentru care aceasta dependenta nu poate fi
neglijata in intervalul optic de frecvente se numesc medii dispersive.
Deoarece la trecerea undei luminoase electromagnetice dintr-un mediu intr-altul, de regula nu se modifica frecventa sau perioada undei ci viteza acesteia, putem deduce simplu modificarea lungimii de unda la aceeasi frecventa prin trecerea luminii din vid in mediul material. Se obtine:
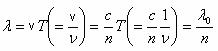
unde ![]() si
si ![]() sunt lungimile de
unda ale luminii in mediu, respectiv in vid.
sunt lungimile de
unda ale luminii in mediu, respectiv in vid.
Daca descriem o unda
a intr-un mediu, in general, prin proarea fara amortizare
cu viteza v a perturbatiilor armonice aflate in faza, din toate
punctele unui , pe directia perpendiculara pe , atunci
ecuatia undei e exprima faptul ca perturbatia
armonica la momentul t intr-un perpendicular pe directia de
proare, situat la distanta x de ul sursa coincide cu
perturbatia momentana din acest la momentul ![]() , unde
, unde ![]() este timpul necesar proarii
perturbatiei pe directia axei Ox de la ul sursa la ul
curent considerat la distanta x. Indiferent de natura marimilor
definite in si supuse perturbatiilor armonice in ul
sursa pentru care alegem x = 0 se obtine o evolutie a
perturbatiilor de tipul :
este timpul necesar proarii
perturbatiei pe directia axei Ox de la ul sursa la ul
curent considerat la distanta x. Indiferent de natura marimilor
definite in si supuse perturbatiilor armonice in ul
sursa pentru care alegem x = 0 se obtine o evolutie a
perturbatiilor de tipul :
![]()
astfel ca ecuatia undei care descrie dependenta perturbatiei de pozitia x si timpul t capata forma
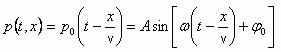
A este
amplitudinea perturbatiilor sursei, ![]() pulsatia acestora,
pulsatia acestora, ![]() faza initiala si
faza initiala si ![]() faza momentana la nivelul sursei.
faza momentana la nivelul sursei.
In ecuatia undei e ![]() , A isi pastreaza semnificatia iar faza
undei depinde de pozitia x a ului si timp dupa legea
, A isi pastreaza semnificatia iar faza
undei depinde de pozitia x a ului si timp dupa legea
![]()
Folosind relatiile cunoscute pentru perturbatiile armonice si anume
![]() ,
, ![]() ,
, ![]()
(cu K marimea vectorului de unda) putem rescrie faza momentana a undei sub forma :
![]()
.
Daca
exprimam lungimea de unda ![]() a undelor prin
lungimea de unda in vid
a undelor prin
lungimea de unda in vid ![]() si indicele de
refractie n al mediului de proare
si indicele de
refractie n al mediului de proare ![]() , obtinem urmatoarea exprimare a fazei :
, obtinem urmatoarea exprimare a fazei :
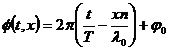
care pune in
evidenta produsul ![]() cu ajutorul carui se exprima drumul optic.
cu ajutorul carui se exprima drumul optic.
Drumul optic diferential se
exprima prin produsul dintre indicele de refractie al mediului
strabatut de lumina si lungimea arcului diferential pe
traiectorie, toate luate intr-un punct P al traiectoriei, ![]() .
.
Integrala acestei forme diferentiale pe traiectoria razei de lumina, intre doua puncte P1 si P2 reprezinta marimea drumului optic parcurs de lumina pe traiectoria razei de lumina, intre punctele P1 si P2.
Daca indicele mediului este constant drumul optice devine egal cu produsul dintre indicele de refractie si lungimea drumului geometric parcurs pe traiectorie
![]()
![]()
In final este important sa mentionam ca legea a doua a refractiei si implicit legea Snell Dessectiunes exprima, in optica electromagnetica, relatia de continuitate la traversarea suprafetei de separare a mediilor, pentru componenta tangentiala a vectorilor de unda (in cele doua medii).
Amintim ca vectorul de unda
K pentru o unda monocromatica are modulul ![]() si directia si sensul vitezei
de proare.
si directia si sensul vitezei
de proare. ![]() este un vector
constant in cazul undei e monocromatice.
este un vector
constant in cazul undei e monocromatice.
In ura 6 se reprezinta vectorii de unda pentru undele e incidente si refractate. Cei doi vectori fac cu normalele unghiuri egale cu cel de incidenta (i1), respectiv de refractie (i2). Se considera refractia luminii la trecerea din vid (1) in mediul material (2)
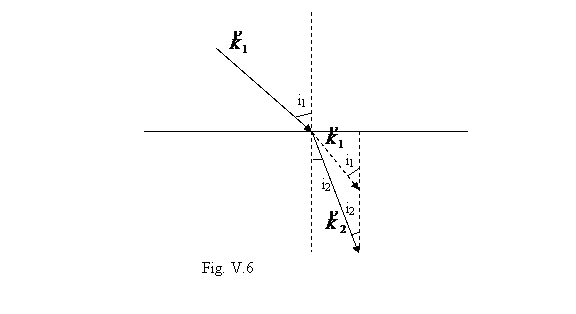
Conditia de continuitate pentru componenta tangentiala a vectorului de unda conduce la egalitatea proiectiilor acestor vectori pe ul de separare a mediilor:
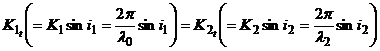
ceea ce implica
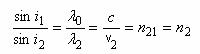
Conductibilitatea electrica Mierea italiana uniflora (L. Persano O\'ddo - 28/426) de castanea, citrus, eucaliptus, arbutus, erica helianthus au [...] |
METODE SI MIJLOACE DE MASURARE IN ANTROPOMETRIA CAPULUI 1 Consideratii generale Masurarea dimensiunilor capului nu pot fi decat aproximati [...] |
Indici de refractie. Definitii. Proprietati. 1. Definirea indicilor de refractie relativi si absoluti in optica geometrica Refra [...] |
Copyright © 2010 - 2024
: eSanatos.com - Reproducerea, chiar si partiala, a materialelor de pe acest site este interzisa!
Informatiile medicale au scop informativ si educational. Ele nu pot inlocui consultul medicului si nici diagnosticul stabilit in urma investigatiilor si analizelor medicale la un medic specialist.
Termeni si conditii - Confidentialitatea datelor - Contact